Four problem-solving steps

I was watching a YouTube clip last year which outlined a series of mathematical problem-solving steps from Hungarian emigré George Pólya, Stanford University professor of mathematics from 1940 to 1953 (The Math Sorcerer, 2022). In 1945 Pólya wrote a book on problem solving (1957) which we can view in its second edition online at the OpenLibrary here.

The really interesting thing is that the process which Professor Pólya outlines is useful for solving almost any problems, not simply those on mathematics. He outlines the key elements for each section as follows (1957):

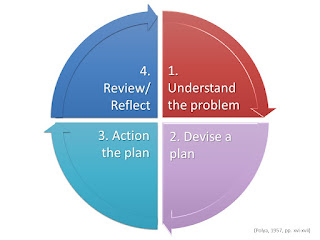
Step 1: Understanding the problem. We need to work out what the problem is. What don't we yet know? "What are the data" that we need to know? What are the problem elements or parameters? Can we work out what the elements/parameters are? If we can work out the elements, does that give us enough information to work out what "the unknown[s are]?" Or not? Is any information "redundant? Or contradictory?" Map out the relationships: create a mind map, or a concept map (see here). "Separate the various" problem elements. Formalise them in writing (Pólya, 1957, p. xvi). Until we are sure that know and understand the problem, we cannot move to the second step.

Step 2: Devise a plan. We need to ask ourselves if we have "seen [the problem] before?" Perhaps we have experienced "the same [type of] problem in a slightly different form?" Or maybe we have experienced "a related problem?" (and could reuse the solution, or the method, we developed for that). Or perhaps we are aware of a theory or a model "that could be useful?". We need to examine "the unknown! And try to think of a familiar problem having the same or a similar unknown. [... can we] introduce some auxiliary element in order to make its use possible? Could [we] restate the problem [or part of the problem]?" (Pólya, 1957, p. xvi). We need to define all the parameters so we can work out the scope of the problem. If [we] cannot solve the proposed problem [we can instead] try to solve [a] related problem." Is there "a more accessible related problem? A more general problem? A more special problem? An analogous problem? Could [we] solve a part of the problem? [...] Could [we] think of other data appropriate to determine the unknown?" Can we "change the unknown or the data, or both if necessary, so that the new unknown and the new data are nearer to each other?" We can ask ourselves if we used "all the data?" All the parameters/elements? "Have [we] taken into account all essential notions involved in the problem?" (Pólya, 1957, p. xvii). We need to end up in a place where we know how the data and the unknown are connected. Once we know that, then we can move onto step 3.

Step 3: Action the plan. Now we need to action our plan. We need to "check each step" to ensure we are on track, and that our assumptions are realistic. Can [we] see clearly that the step is correct? Can [we] prove that it is correct?" (Pólya, 1957, p. xvii). We need to look for reassurance each time we put our next move - step 4 - into play.

Step 4: Reviewing/Reflecting. Here is where we review "the solution [we have] obtained". "Can [we] check the result? Can [we] check the argument? Can [we] derive the result differently? Can [we] see [the solution] at a glance? Then we need to consider if we can "use the result, or the method, for [a future] problem?" Can we formalise our process to reuse it? And, like most reflections, this work needs to be honest, objective, and developmental (Pólya, 1957, p. xvii).

I am sure we can all see that this process is not limited solely to mathematics. This approach can be used for any type of problem solving.

Sam

References:

Pólya, G. (1957). How to solve it: a new aspect of mathematical method (2nd ed.), Doubleday.

The Math Sorcerer. (22 July 2022). 4 Steps To Solve Any Problem [video]. YouTube.  https://www.youtube.com/watch?v=rBa9R32IHxI